Estimating the Mechanical Yield for Labour's Proposed Tax System

economics

After creating a model for the UK’s income distribution, I can now estimate the mechanical yield for arbitrary tax systems.

Firstly, I would like to anounce some adjustments I’ve made to the previous model. I’ve switched from using Chotikapanich’s model for income distribution and have instead moved to one proposed Rasche et al. that corresponds with the Pareto distribution. These changes were somewhat necessary since the previous model had income capped at around £75K which doesn’t represent reality. The old model had considerable error which is virtually eliminated with this new model.

Chotikapanich's Model Rasche's Model

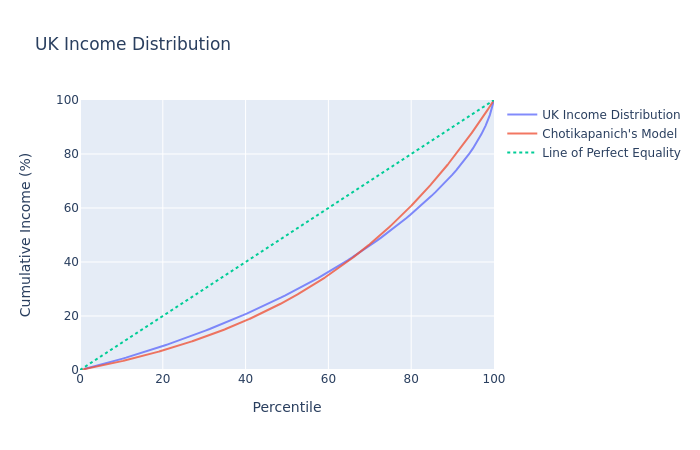
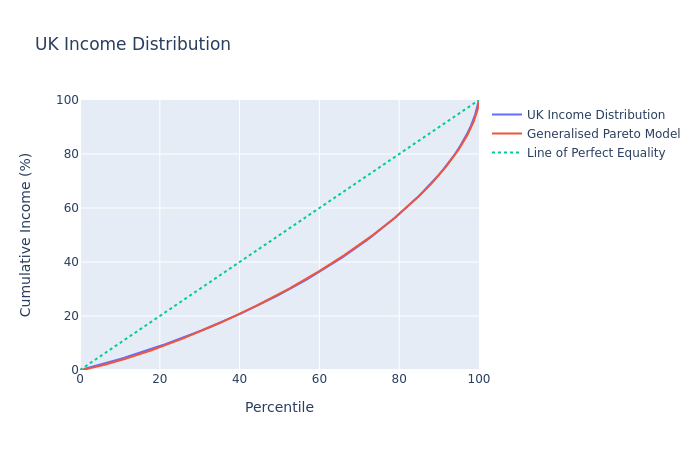
I fit the model to the ONS income distribution data for the financial year ending 2018 to receive

$$\alpha = 0.630$$ $$\beta = 0.820$$

Aside from the changes in the income distribution model, I also made minor changes to some of the calculations. Previously, the calculation for the income of an indivdual at a certain point p was

$$L(p) - L(p - \frac{1}{\text{TaxPayers}})$$

where TaxPayers is equal to the number of tax payers in the economy and L is the equation for the Lorenz curve of the same economy. The calculation for the wealth of this individual is now

$$\text{TaxPayers} \cdot \frac{dL}{dp}(p)$$

or alternatively written

$$\text{TaxPayers} \cdot L’(p)$$

where L' is the derivative of L.

In the case of Rasche’s ‘General Pareto’ model, this derivative is equal to

$$ \frac{\alpha}{\beta} \cdot (1 - (1 - x)^a)^{\frac{1}{\beta}} \cdot (1 - x)^{\alpha - 1}$$

This change in the method of calculation is better for the model since it’s defined everywhere that the derivative is defined and is continuous wherever the derivative is continuous, this change makes the function easier to work with.

In order to calculate the mechanical yields, I had to first define tax functions. The code for calculating the tax of an individual at point p is as follows

 def tax(self, p):
    income = self.income(p)
    allowance = standard = 12500
    if income > 100000:
        allowance = allowance - (income - 100000)/2
        allowance = np.maximum(0, allowance)
 
    tax = 0
    rates = {
        (0, 12500): 0,
        (12500, 50000): 0.2,
        (50000, 150000): 0.4,
        (150000, float('inf')): 0.45
    } 

    for (l, u), rate in rates.items():
        l = l + (allowance - standard)
        u = u + (allowance - standard)
        taxable = np.minimum(u - l, income)
        income -= taxable
        tax += taxable * rate

        if income <= 0:
            return tax

    return tax

The tax function was built using current tax brackets which can be found on the UK Government website. The code also takes into account the fact that the personal allowance decreases progressively for individuals earning over £100,000.

The code for the tax function corresponde to Labour’s tax proposed tax system is essentially the same as the one for the current tax system, however I changed the rates to match the ones that the Labour party proposed. The definition for the rates is as follows

rates = {
    (0, 12500): 0,
    (12500, 50000): 0.2,
    (50000, 80000): 0.4,
    (80000, 125000): 0.45,
    (125000, float('inf')): 0.5,
}

The source used for Labour’s tax plans were its 2019 Manifesto Costings and I used the Labour party’s ‘Fair Tax Calculator’ to make sure my code was giving correct values.

The code for calculating the total tax revenue given a tax function tax is

$$\text{TaxPayers} \cdot \int_0^1 \text{tax}(x) dx$$

where TaxPayers is again the number of income tax payers in the economy. In applying this function I receive a value of £189bn which is quite close to the actual figure of £180bn however I would like to be as close as possible. I suspect the error is could in part be due to an incorrect definition of the tax function but more importantly, I haven’t dealt with tax deductions and the fact that Scotland has different tax rates so before doing any further work, I’ll attempt to reduce the error by considering some of these.

Using the labour tax function defined in terms of the Labour Party’s proposed tax system, I estimate a yield of £193.7bn which is an increase of £13.7bn from the actual £180bn collected in 2018. This is quite similar to the Labour Party’s own estimate of £11.4bn which is the figure they get before accounting for Scotland and behavioural effects. My estimate may be slightly larger due to the fact that the amount of income tax collected each year tends to increase a bit each year while I assumed it would remain the same.

To get a more accurate total, I’d need to also consider that total income isn’t necessarily taxable income especially for richer individuals. The IFS and the Labour party account for this by scaling income down by a factor of 10. I’ll also have to deal with behavioural changes in response to a hypothetical implementation of Labour’s proposed tax changes, for which I’ll have to do some extra reading to understand accurately.

After doing these, I’ll be able to estimate the amount of income tax the government would be able to collect under the current tax system and compare it to the amount that would be raised under the proposed Labour tax plan.

Estimating the Mechanical Yield for Labour's Proposed Tax System

References